18.11.2011 11:39:13
Topic:
The param "a" in the Simplified Parabolic Formula
admin
Administrator
Posts: 4
|
The implementation of the simplified parabolic formula has a subtle issue regarding the parameter a which is defined as follows:
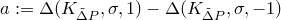
In case of the non-premium adjusted version, this is straightforward as this parameter is either the foreign discount factor or 1.0. However, for the premium adjusted spot version the parameter a reduces to
There seems to be a circular argumentation in this version:
- the volatility for the delta strike is not known until the calibration is finished
- the volatility is needed for the calculation of the strike
- without the strike we can not calculate the parameter a
This paradox can be resolved, by remembering that the simplified parabolic function has been designed such that the volatility for a put delta of
is:
Given the smile strangle at each step of the calibration this is the volatility for the strike
This allows a straightforward implementation:
- given the volatility above, we can calculate the corresponding delta strike
- given the strike we can calculate the parameter a
Any further questions are welcome!
|
|
|
17.11.2011 17:33:37
Topic:
Strike Delta Conversion in C++
admin
Administrator
Posts: 4
|
The following discussion is based on the C++ code implemented in FxTests. The code is a contribution to QuantLib, the open source library for quantitative finance applications. The code is likely to be added in one of the next releases.
To use the code, download and unzip the linked file. Make sure you have the latest QuantLib and boost installation, otherwise you will not be able to use the code. An installation guide is available at http://quantlib.org/install/vc9.shtml
After downloading, change the include and library directories to the directories of your QuantLib/boost installations.
In the first discussion, we will explain the functionalities of the BlackDeltaCalculator class. In particular, we will show how to handle the different delta types and how to calculate strikes from a given delta. In the main file, the market variables are set up first.
Real tau=0.5;
Real rd=0.033, rf=0.012;
Real spot=1.49122;
Real vol=0.145;
Real stdDev=vol*std::sqrt(tau);
Real domDiscount=std::exp(-rd*tau);
Real forDiscount=std::exp(-rf*tau);
The BlackDeltaCalculator accepts discount factors and a standard deviation to avoid any time to maturity issues. Consequently, the user can calculate the time to maturity in any way and use the result for the calculation of the discount factor and standard deviation.
BlackDeltaCalculator bdc(Option::Call, DeltaVolQuote::PaFwd,spot, domDiscount, forDiscount,stdDev);
The constructor accepts the option type (Option is a QuantLib class), the delta type (implemented as an enumeration in the DeltaVolQuote class), the spot, the domestic/foreign discount and the standard deviation, which is
In our case we have chosen the premium adjusted forward delta. In the next step, we will calculate the delta for a strike with the deltaFromStrike function. Given the calculated delta, we will extract the original strike by calling the strikeFromDelta function.
Real strike, callDelta, putDelta;
strike=1.51224; std::cout " -----Forward Premium Adjusted Delta Calculations --------" std::endl;
callDelta=bdc.deltaFromStrike(strike);
std::cout "Call Delta from Strike:" callDelta std::endl;
Real calcStrike=bdc.strikeFromDelta(callDelta);
std::cout "Strike from Delta:" calcStrike std::endl;
The output at this stage will be
-----------Forward Premium Adjusted Delta Calculations --------------
Call Delta from Strike:0.467614
Strike from Delta:1.51224
Obviously, the original strike is returned. In the next step we will call the putCallParityValue function, which calculates the difference of the put and call delta for a given strike K for any delta type. The code which achieves this is
Real putCallParVal=bdc.putCallParityValue(strike);
bdc.setOptionType(Option::Put);
putDelta=bdc.deltaFromStrike(strike);
std::cout "Expected Put Call Parity Value:" callDelta-putDelta std::endl;
std::cout "Calculated Put Call Parity Value:" putCallParVal std::endl;
The code calculates the call and put delta manually and compares the difference to the result provided by the putCallParityValue function. In the code, we have changed the underlying option type with setOptionType to a put.
The output at this stage is
Expected Put Call Parity Value:1.0035
Calculated Put Call Parity Value:1.0035
Finally, we show how the at-the-money strike can be calculated. The corresponding function is atmStrike. The function accepts an at-the-money type, such as ATM-Forward or ATM-Delta-Neutral. As before, the at-the-money types are specified in the DeltaVolQuote class. The calculation of the at-the-money strike for the forward and delta-neutral atm-types is
std::cout "Atm Fwd Strike:" bdc.atmStrike(DeltaVolQuote::AtmFwd) std::endl;
std::cout "Atm DN Strike:" bdc.atmStrike(DeltaVolQuote::AtmDeltaNeutral) std::endl;
The output of this part is:
Atm Fwd Strike:1.50696
Atm DN Strike:1.49906
To perform the same calculations for the spot delta, we can use the setDeltaType function:
bdc.setDeltaType(DeltaVolQuote::Spot);
The same operations as above can be used to calculate the spot delta variables. The output is
----------- Spot Delta Calculations --------------
Call Delta from Strike:0.503811
Strike from Delta:1.51224
Expected Put Call Parity Value:0.994018
Calculated Put Call Parity Value:0.994018
--------------------- ATM Calculations --------------------
Atm Fwd Strike:1.50696
Atm DN Strike:1.5149
edited by admin on 18.11.2011
|
|
|
17.11.2011 17:32:18
Topic:
When do we need to adjust for the premium?
admin
Administrator
Posts: 4
|
In the previously discussed working paper, we provide a reference to the following table of volatility quoting conventions for different currency pairs.
FX Quoting Conventions
Currency PairPremium CurrencyConvention
EUR-USD USD regular
USD-JPY USD premium-adjusted
EUR-JPY EUR premium-adjusted
USD-CHF USD premium-adjusted
EUR-CHF EUR premium-adjusted
GBP-USD USD regular
EUR-GBP EUR premium-adjusted
AUD-USD USD regular
AUD-JPY AUD premium-adjusted
USD-CAD USD premium-adjusted
USD-BRL USD premium-adjusted
USD-MXN USD premium-adjusted
While this conforms with our knowledge of quoting conventions, there are data providers which use different conventions. We would be interested in any opinions where and which conventions do not agree with the ones shown above. Sources which discuss the conventions seem to be rare. Any references are welcome!
edited by admin on 18.11.2011
|
|
|
17.11.2011 17:16:30
Topic:
Strike-Delta Conversion
admin
Administrator
Posts: 4
|
The first post discusses issues occurring in the calculation of strikes from a given delta and volatility. An introduction to the topic is given in our working paper FX Volatility Smile Construction . There are 4 types of Deltas in the FX markets:
- Spot Delta
- Forward Delta
- Spot Delta Premium-Adjusted
- Forward Delta Premium-Adjusted
We will denote the deltas by ,, and respectively.
The problem discussed here arises in the calculation of the strike given the delta and volatility . This is a straightforward procedure for the first two delta types, as there are closed form solutions available:
with being the inverse normal CDF. This is not the case for the last two delta types. For example, the premium-adjusted spot delta can be represented as follows
One can see that the strike appears outside and inside the normal CDF such that a numerical procedure has to be employed for the strike from delta calculation.
However, a more problematic issue of this calculation is found by looking at the plot of the premium-adjusted delta. The Figure below shows a plot of a premium-adjusted and standard call delta versus the strike.
Premium-Adjusted Spot Call Delta (lower chart) and Standard Call Delta (upper chart)
A problem that occurs is that the strike-delta function is not a one-to-one mapping for the premium-adjusted case. For example, given a premium-adjusted delta of 0.25 would result in two strikes which yield the same delta. Where would this problem occur? Imagine that you have a delta-volatility smile which accepts a premium-adjusted delta and returns the corresponding volatility. Moving from delta-vol to strike-vol space requires the calculation of the strike corresponding to the given delta-vol pair. The result in the premium-adjusted case would be two strikes instead of one strike. The volatility-strike mapping would not be unique.
Proposed Solution Clearly, a choice has to be made. We choose to search for a strike which is on the right side of the strike corresponding to the maximum of the premium-adjusted delta; we are looking for strikes to the right of in the upper chart. The first reason for this choice is that the mapping strike versus delta is unique in this area. Also, the most common application is to search for strikes given an out of the money call delta such as 0.10 or 0.25. The strikes on the right side of the strike corresponding to the maximum will have an intuitive interpretation as out of the money strikes if the non-premium-adjusted delta is out of the money too. For example, assume that the at-the-money strike is 100 and the strike corresponding to a spot delta of 0.25 is 126. The premium-adjusted delta is calculated by adjusting the non-premium-adjusted delta by the premium. Assume that this adjustment results in a premium-adjusted delta of 0.21. To reveal the strike of the non-premium-adjusted position one should look in the area proposed above. Looking on the left side of will yield a strike of 20 which is a deep in the money call position and not an out-of-the-money position.
Why not to the right of the at-the-money strike? Consider the figure below, where we have a random market situation. The shadowed area indicates again the region where we propose to look for a strike. This picture also shows the at-the-money point, which in this case is at-the-money spot.
Looking for a strike to the right of the spot level would not solve the problem that two strikes are found for the same delta. The problem would still occur for high deltas, such as 0.65. The numerical procedure would converge to one of the strikes depending on its starting value.
C++ Code A C++ implementation of delta to strike conversions will be presented and discussed in one of the next discussions.
edited by admin on 17.11.2011
edited by admin on 17.11.2011
|
|
|